前回書いた扇形状にアニメーションする記事、非常に残念な動きをしています。無念としか言いようがありません。
これを機におさらいをしてみようと、過去の薄れかけている記憶を呼び覚まし、高校数学の「三角関数」を調べてきました。
円弧上の点の座標を求める必要がある場合、これの理解がもう必須なんですよね。「Math.sin(x)」とかで値だけ出すことは可能なのですが、そもそも関係を理解していないと正しく関数を組めません。
sin、cos、tanの基本の公式
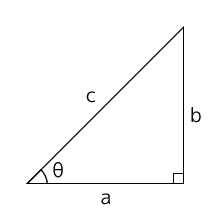
このような直角三角形の場合、三角関数の公式でそれぞれの場所の長さや角度を求めることが出来ます。(三角形は必ず直角三角形である必要があります。)
これはもう公式なので覚えるかメモしてください。
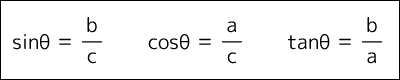
例えばそれぞれの値がこうなっていた場合は、公式に当てはめるとこうなります。
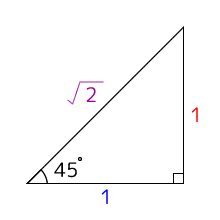
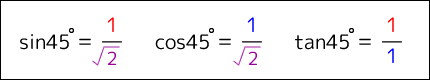
<例題>
sinを使用してXの長さを求めます。
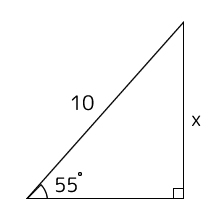
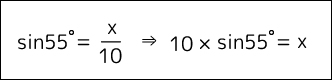
そのまま公式にあてはめ、=の両方に10をかけると、Xの長さは「10 × sin55°」が正解となります。
円弧上の点を求める三角関数
ここから数Ⅱの範囲になってきます。半径rの円で角度がθの時、点rの座標を求めます。
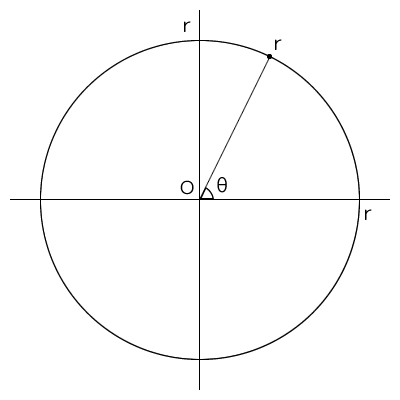
<点rの座標を求める>
点rのx座標を求めるにはcos、y座標にはsinを使います。
図に、xy軸に直角になるように赤い線を書き足すと、座標が求めることができます。
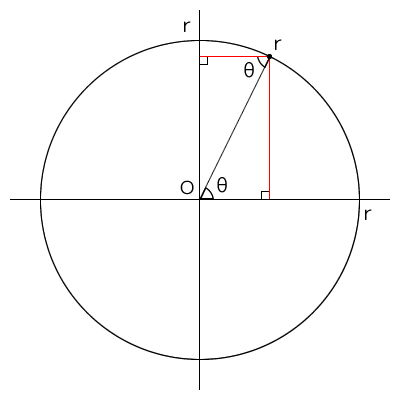
赤線とx軸の線は平行線になるので、赤線と線ORとの間の角度はθで同じですね。
線ORは円の半径と同じで1なので、公式に当てはめて、例題と同様に分解すると…
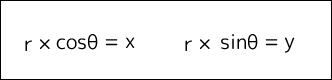
点rの座標は(r*cosθ,r*sin)となるわけです。
次回はこちらをプログラム用に落とし込むところをできたらなと思います。(ラジアンという新しい単位が出てきます…)










